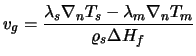Control Tasks
 Low temperature
gradients have the unpleasant effect that the process reacts very
sensitively to disturbances. High temperature gradients stabilize the
crystal shape at the crystallization front, sure enough at the expense
of crystal grid quality. Fundamental in the VCz-process is
minimization of the temperature gradients. This renders diameter control a difficult task.
Even weak disturbances lead to uncontrolled
growth which cannot be handled by (too) slow controllers.Thus, it is not
possible to control the process with conventional approaches based on
linear theory. Even methods based upon newer insights, e.g. those presented
in [Bardsley
et.al.], [Gevelber et.al.], fail. Low temperature
gradients have the unpleasant effect that the process reacts very
sensitively to disturbances. High temperature gradients stabilize the
crystal shape at the crystallization front, sure enough at the expense
of crystal grid quality. Fundamental in the VCz-process is
minimization of the temperature gradients. This renders diameter control a difficult task.
Even weak disturbances lead to uncontrolled
growth which cannot be handled by (too) slow controllers.Thus, it is not
possible to control the process with conventional approaches based on
linear theory. Even methods based upon newer insights, e.g. those presented
in [Bardsley
et.al.], [Gevelber et.al.], fail.
|
Crucial for the whole process is the trend of the growth velocity 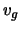 and the pulling velocity and the pulling velocity 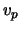 . In order to produce a crystal of given shape both growth and pulling velocity have to follow a given trajectory. This can be seen by the following equations, which describe the behaviour of the crystal radius and its angle: . In order to produce a crystal of given shape both growth and pulling velocity have to follow a given trajectory. This can be seen by the following equations, which describe the behaviour of the crystal radius and its angle:
where
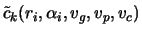 and and
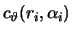 are functions of the interface radius are functions of the interface radius 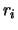 , the growth angle , the growth angle 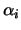 , and the velocities. , and the velocities.
If a special crystal shape is given, e.g. in terms of a function
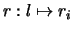 with with
![$ l \in [0, L]$](gif/img18.gif) and and
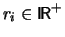 for a crystal of length for a crystal of length 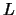 , it is possible to derive expressions for the growth velocity , it is possible to derive expressions for the growth velocity 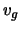 and the pulling velocity and the pulling velocity 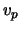 of the type of the type
Here 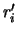 and and 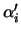 stand for the first derivative of the radius and the growth angle with respect to the length stand for the first derivative of the radius and the growth angle with respect to the length 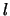 , respectively. , respectively.
As shown above one should focus attention on the correct choice of the pulling and the growth velocity.
Pulling velocity:
This case is not too difficult to handle, since the pulling velocity is available for control. It acts fast and can be used to compensate high frequency disturbances. For this purpose an observer is required. This is the matter of the next section.
Growth velocity:
Manipulation of this variable is quite a complex task because the growth velocity is not available for control. One has to take a closer look on the physical relations: From a heat balance over the crystallization front it is possible to derive the following equation describing the dependency of
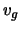 on the temperature fields within melt and cyrstal: on the temperature fields within melt and cyrstal:
In this equation, which is derived assuming a planar growth interface,
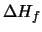 stands for the specific latent heat, stands for the specific latent heat, 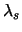 , , 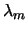 are the heat conductivities of solid and liquid GaAs, and are the heat conductivities of solid and liquid GaAs, and
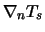 , ,
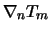 are the temperature gradients within the crystal and the melt normal to the growth interface. This leads to the following are the temperature gradients within the crystal and the melt normal to the growth interface. This leads to the following
 - Question:
- Is it possible to manipulate
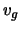 by the heat flow into the system in such a way that the crystal grows according to the desired shape? by the heat flow into the system in such a way that the crystal grows according to the desired shape?
- Possible solution:
- Modelling of the whole thermal system.
Disadvantages:
- All heat flows must be taken into account (complex models);
- Many uncertain parameters;
- Many uncertain boundary conditions;
- Thermal models are only valid for a special configuration.
|
- Alternative:
- Find basic relations describing the behaviour of the system in quality, make use of ``unconventional'' control variables (accessed by observers), make use of robust PID-approaches.
Conclusion
Two control concepts are presented:
In both cases information about the state of the process is required
 state observer. state observer.
|


 Low temperature
gradients have the unpleasant effect that the process reacts very
sensitively to disturbances. High temperature gradients stabilize the
crystal shape at the crystallization front, sure enough at the expense
of crystal grid quality. Fundamental in the VCz-process is
minimization of the temperature gradients. This renders diameter control a difficult task.
Even weak disturbances lead to uncontrolled
growth which cannot be handled by (too) slow controllers.Thus, it is not
possible to control the process with conventional approaches based on
linear theory. Even methods based upon newer insights, e.g. those presented
in [
Low temperature
gradients have the unpleasant effect that the process reacts very
sensitively to disturbances. High temperature gradients stabilize the
crystal shape at the crystallization front, sure enough at the expense
of crystal grid quality. Fundamental in the VCz-process is
minimization of the temperature gradients. This renders diameter control a difficult task.
Even weak disturbances lead to uncontrolled
growth which cannot be handled by (too) slow controllers.Thus, it is not
possible to control the process with conventional approaches based on
linear theory. Even methods based upon newer insights, e.g. those presented
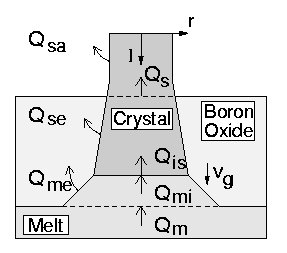
in [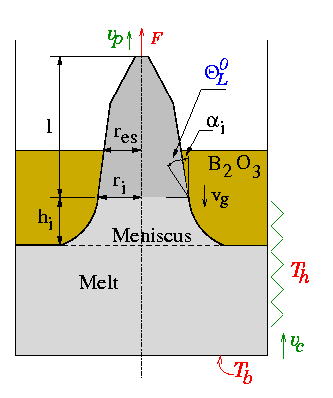 The figure in the right shows the basic variables of the process. The following measurements are available:
The figure in the right shows the basic variables of the process. The following measurements are available: